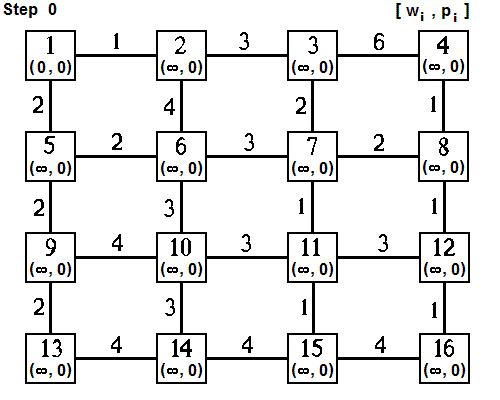
| Dijkstra's Algorithm | Base Network: Initialization | Next [Step 1] | Final Step |

| Dijkstra's Minimum Path Algorithm An interactive, graphical depiction generates the minimum path tree (MPT) for Node 1. Note that the permanent label of the MPT origin was set to 0 and the predecessor node to 0; temporary labels for all other nodes were set to ∞ and predecessor nodes to 0. Each algorithm step corresponds to the selection of one node as part of the MPT. The node selected receives a permanent label, w*(i), representing the cumulative cost to that node from the tree origin; this node becomes the start-node for the next step. All outbound links (i,j) from this node are listed as candidates for inclusion on the MPT. For the end-node of each of these links, the corresponding temporary label, w(j), is updated by taking the minimum of the current temporary label, w(j), or the sum of the link cost c(i,j) plus the cumulative cost, w*(i), from the link start-node. If the temporary label is updated, the predecessor node is updated to reflect this improved path. All links that have not been added to the MPT or deleted from further consideration (this occurs if the end node has already been reached via a shorter path) are considered for selection, not only those links just added. The minimum total cost (minimum temporary label) of all nodes opened is always selected. |