Homework 3 -- Shortest Path Algorithms / Skim Trees [ S O L U T I O N ]
Problem 1. Network Characteristics [10 points]
Depicted below is the corrected 2020 Miasma Beach network. Using the network map and the information in Task 1 Table 1, convert speeds and distances to travel times. Produce a network map depicting link distance, speed, and travel time annotated on each link. You may use TransCAD to complete the calculations and produce the final labeled network, but you must do this work individually.
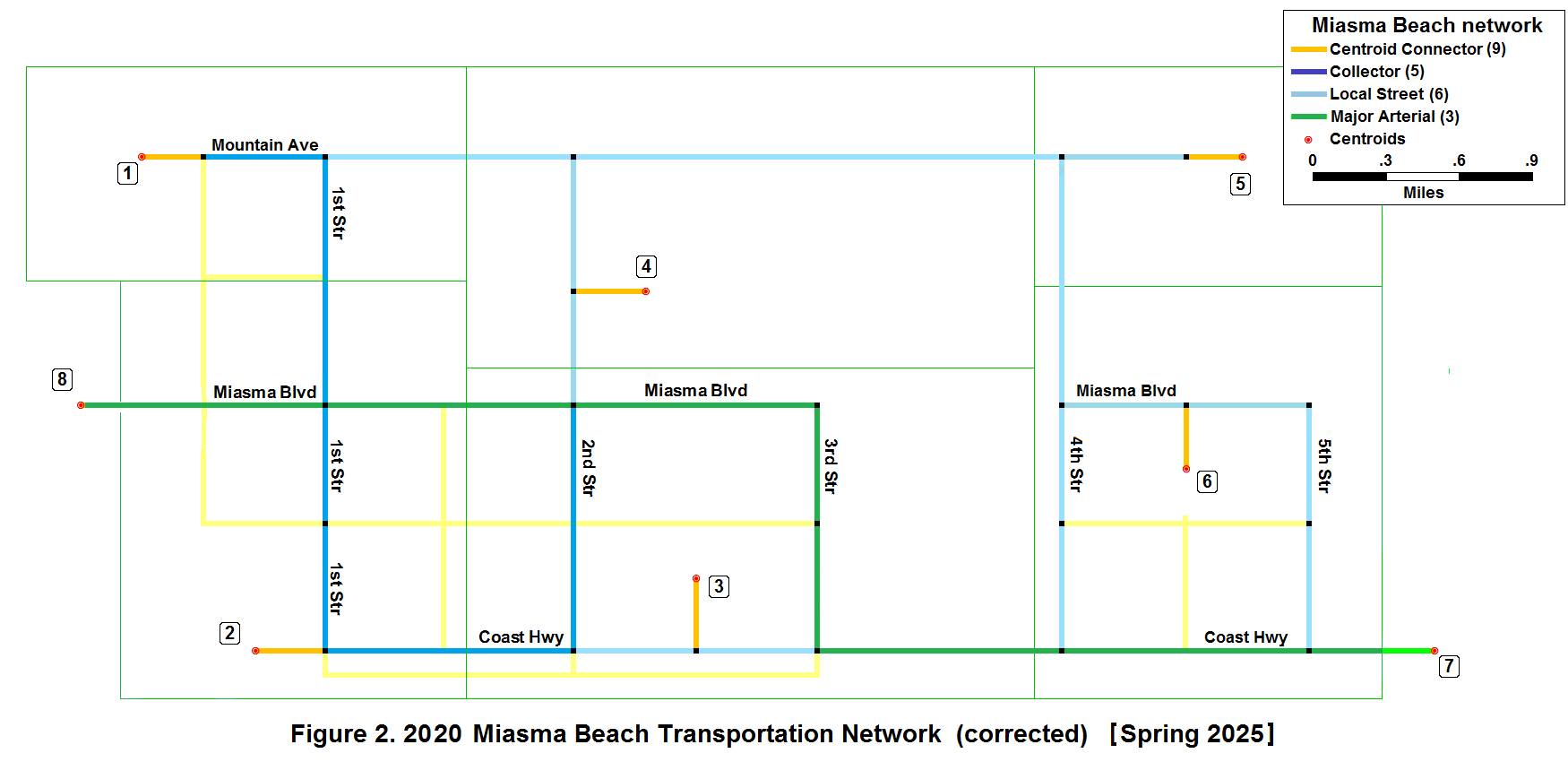
Solution:
Distances are converted using speeds by facility type from Table 1 of the
Miasma Beach problem statement. Resulting travel times (in minutes) and distance
(in miles) are displayed in the Figure below.
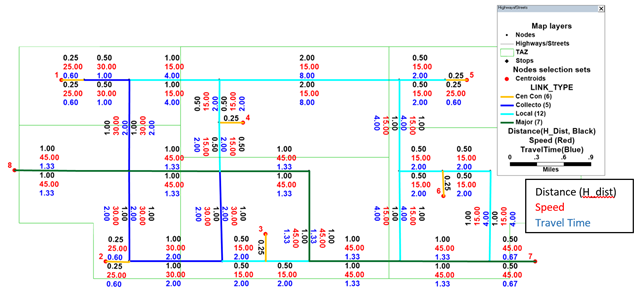
3. Major Arterials: 45 mph = 0.75 miles/min = 1.33 min per mile 4. Minor Arterials: 45 mph = 0.75 miles/min = 1.33 min per mile 5. Collector Street: 30 mph = 0.50 miles/min = 2.00 min per mile 6. Local Streets: 15 mph = 0.25 miles/min = 4.00 min per mile 9. Centroid Connect: 25 mph = 0.42 miles/min = 2.40 min per mile
Problem 2. Performance Analysis (20 points)
Below is the 2000 Miasma Beach transportation network with observed 2000 traffic volumes (kvph by direction) for the PM peak hour (5-6 PM). Calculate link performance characteristics (VMT, VHT, speed) and summarize results by link facility type as well as network-wide totals for VMT, VHT, and average speed. Do not include centroid connectors. Use the BPR link performance function to estimate link travel times based on observed volumes (use defaults for α and β): [ t = t0(1+α(vol/cap)β) ]. Use the spreadsheet provided ( xlsx ).
Computation of Level-of-Service (LOS) can be complex and varies by facility type. Typically, freeway sections utilize link traffic density while arterials utilize link average speed and average time spent following. To simply analysis, use the density-based assessment for all links.
Table 3.12 Density Ranges for Freeway LOS
-------------------------------------------
Level of Service Density Range
(A-F) (veh/mi/lane)
-------------------------------------------
A 0 - 11
B > 11 - 18
C > 18 - 26
D > 26 - 35
E > 35 - 45
F > 45
-------------------------------------------
Describe any 2000 network problems. Consider LOS and observed volume/capacity ratios as a possible congestion measure. Summarize 2000 observed VMT, VHT, and average speed (total and by facility type).
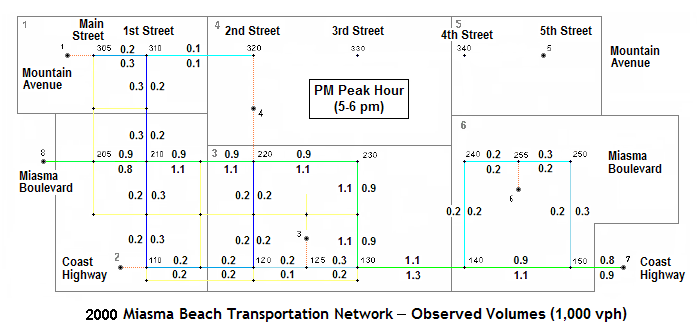
Solution: [ results ]
The attached file summarizes the calculated
performance for the observed flows. The spreadsheet used the free flow speeds
(in minutes/mile) and link length with observed volumes, base capacities, to
estimate congested travel times corresponding to observed link travel times.
Vehicle-miles traveled (VMT) and vehicle-hours traveled (VHT) are computed by
link and by facility type.
Analysis of observed flows suggest that only SR-1 is congested (severely).
Problem 3. Minimum Paths (20 points)
Apply Dijkstra's Algorithm by hand, as illustrated in class, for either part 3A or 3B:
- Find two minimum path trees for a single centroid (1-6) from the
Miasma Beach network, using travel times from Problem 1 for one
skim tree and distance for the second. Compare the two skim trees
(since link speeds vary, so may the resulting skims). You can verify
your results with TransCAD.
- Find the minpath trees for three centroids from the
in-class network (you must use centroids 2, 3, or 4).
Include tables and plots that should approximate presentation standards. Use either the table format or the graph format (see skim tree). Include a plot of the minimum path (skim) tree for each case. Construct the interzonal travel time matrix (tij) corresponding to the Miasma or class networks, including all computed O-D travel times (or distances), including those from class (as applicable).
- Find two minimum path trees for a single centroid (1-6) from the
Miasma Beach network, using travel times from Problem 1 for one skim tree
and distance for the second. Compare the two skim trees (since link speeds
vary, so may the resulting skims). You can verify your results with TransCAD.
Time and Distance skims Solutions (trees and tables for all 8 TAZs and ESs). Worksheets are not shown for Miasma Beach: see TransCAD results from your Project (Task 2) for details. For full credit, both skims must be provided!
- Find the minimum path tree for three centroids of the in-class network (centroids 2, 3, and 4).
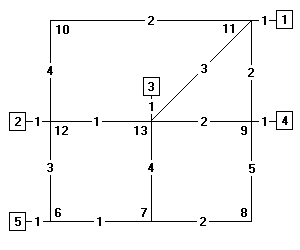
Solution Approach:
Intrazonal travel times are computed as one half the travel time to the closest neighboring zone.Hints: Note that the tabulated cumulative travel time is never decreasing and the number of steps will equal the number of nodes in the network (unless all the desired paths are found prior to closing all other nodes).
Problem 2(c) Class Ex: Travel Time Skims
---------------------------------------
From\to 1 2 3 4 5
---------------------------------------
1 2.0 6 5 4 9
2 6 1.5 3 5 5
3 5 3 1.5 4 6
4 4 5 4 2.0 8
5 9 5 6 8 2.5
---------------------------------------
Shortest Path Worksheet: From Centroid 2
------------------------------------------------------------------
Node Path Length
Step -------- ------------------ Decision Path
From To Cum + Link = Total
------------------------------------------------------------------
1 2 12 0 1 1 1. Add #12 p(12)= 2
------------------------------------------------------------------
2 12 6 1 3 4 4. Add # 6 p( 6)=12
10 1 4 5 6. Add #10 p(10)=12
13 1 1 2 2. Add #13 p(13)=12
------------------------------------------------------------------
3 13 3 2 1 3 3. Add C#3 p( 3)=13
7 2 4 6 5. Del link
9 2 2 4 5. Add # 9 p( 9)=13
11 2 3 5 7. Add #11 p(11)=13
------------------------------------------------------------------
4 C#3 3 At Centroid
------------------------------------------------------------------
5 6 5 4 1 5 8. Add C#5 p( 5)= 6
7 4 1 5 9. Add # 7 p( 7)= 6
------------------------------------------------------------------
6 9 4 4 1 5 10. Add C#4 p( 4)= 9
8 4 5 9 10. Del link
11 4 2 6 6. Del link
------------------------------------------------------------------
7 10 11 5 2 7 7. Del link
------------------------------------------------------------------
8 11 1 5 1 6 11. Add C#1 p( 1)=11
------------------------------------------------------------------
9 C#5 5 At Centroid
------------------------------------------------------------------
10 7 8 5 2 7 12. Add #8 p( 8)= 7
------------------------------------------------------------------
11 C#4 5 At Centroid
------------------------------------------------------------------
12 C#1 6 At Centroid -- Finished!
==================================================================
13 8 7 Step not needed...
------------------------------------------------------------------
Shortest Path Worksheet: From Centroid 3
------------------------------------------------------------------
Node Path Length
Step -------- ------------------ Decision Path
From To Cum + Link = Total
------------------------------------------------------------------
1 3 13 0 1 1 1. Add #13 p(13)= 3
------------------------------------------------------------------
2 13 7 1 4 5 7. Add # 7 p( 7)=13
9 1 2 3 3. Add # 9 p( 9)=13
11 1 3 4 5. Add #11 p(11)=13
12 1 1 2 2. Add #12 p(12)=13
------------------------------------------------------------------
3 12 2 2 1 3 4. Add C#2 p( 2)=12
6 2 3 5 8. Add # 6 p( 6)=12
10 2 4 6 10. Add #10 p(10)=12
------------------------------------------------------------------
4 9 4 3 1 4 6. Add C#4 p( 4)= 9
8 3 5 8 8. Del link
11 3 2 5 4. Del link
------------------------------------------------------------------
5 C#2 3 At Centroid
------------------------------------------------------------------
6 11 1 4 1 5 9. Add C#1 p( 1)=11
10 4 2 6 10. Alt Path to #10
------------------------------------------------------------------
7 C#4 4 At Centroid
------------------------------------------------------------------
8 7 6 5 1 6 7. Del link
8 5 2 7 13. Add # 8 p( 8)= 7
------------------------------------------------------------------
9 6 5 5 1 6 11. Add C#5 p( 5)= 6
------------------------------------------------------------------
10 C#1 5 At Centroid
------------------------------------------------------------------
11 10 6 No new nodes
------------------------------------------------------------------
12 C#5 6 At Centroid -- Finished
==================================================================
13 8 7 Step not needed...
------------------------------------------------------------------
Shortest Path Worksheet: From Centroid 4
------------------------------------------------------------------
Node Path Length
Step -------- ------------------ Decision Path
From To Cum + Link = Total
------------------------------------------------------------------
1 4 9 0 1 1 1. Add # 9 p( 9)= 4
------------------------------------------------------------------
2 9 8 1 5 6 9. Add # 8 p( 8)= 9
11 1 2 3 2. Add #11 p(11)= 9
13 1 2 3 3. Add #13 p(13)= 9
------------------------------------------------------------------
3 11 1 3 1 4 4. Add C#1 p( 1)=11
10 3 2 5 7. Add #10 p(10)=11
13 3 3 6 3. Del link
------------------------------------------------------------------
4 13 3 3 1 4 5. Add C#3 p( 3)=13
7 3 4 7 10. Add # 7 p( 7)=13
12 3 1 4 6. Add #12 p(12)=13
------------------------------------------------------------------
5 C#1 4 At Centroid
------------------------------------------------------------------
6 C#3 4 At Centroid
------------------------------------------------------------------
7 12 2 4 1 5 9. Add C#2 p( 2)=12
6 4 3 7 11. Add # 6 p( 6)=12
10 4 4 8 7. Del link
------------------------------------------------------------------
8 10 12 5 4 9 8. Del link
------------------------------------------------------------------
9 C#2 5 At Centroid
------------------------------------------------------------------
10 8 7 6 2 8 10. Del link
------------------------------------------------------------------
11 7 6 7 1 8 11. Del link
------------------------------------------------------------------
12 6 5 7 1 8 12. Add C#5 p( 5)= 6
------------------------------------------------------------------
13 C#5 8 At Centroid -- Finished
------------------------------------------------------------------
Problem 4. Cost of Network Improvements (10 points)
Based on the 2000 Transportation Study, the City of Miasma Beach expanded the transportation network. Using the cost estimates provided, compute the cost of the network improvements between 2000 (the network in Problem 3) and 2020 (the network in Problem 2). Carefully document all calculations.
Please note that all costs are per lane-mile and that all links improvements and additions must include link costs and the associated intersection costs, plus any development penalties.
Solutions:
Attached is a summary of cost calculations for improvements to the 2000 Miasma Beach network to the 2020 Miasma Beach network. All links are herein tabulated by direction. Intersection costs are only added for one direction. The cost of the more expensive change is used (for example, the new links on upper 3nd and 4th streets use the intersection cost for a Major Arterial at Miasma Blvd but the corresponding cost for a local street at Mountain Blvd). Total link and intersection cost is added and any penaltoies applied. The total cost of upgrades and additions is $4,490,000.00 to produce the 2010 network.Last Updated: 1 May 2025