| Dijkstra's Algorithm | Base Network: Initialization | Next [Step 1] | Final Step |

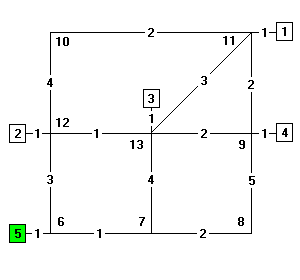
| Dijkstra's Minimum Path Algorithm This interactive, graphical depiction generates the minimum path tree (MPT) for Centroid 5 using Dijkstra's Algorithm. Each step in the algorithm corresponds to the selection of one node as part of the MPT (a label-setting algorithm). The node selected receives a permanent label w*(i) representing the cumulative cost to that node from the tree origin (this node becomes the start-node for the next step). All outbound links (i,j) from this node are listed as candidates for inclusion on the MPT. For the end-node of each of these links, the temporary label w(j) is updated by taking the minimum of the current temporary label w(j) (initially set to ∞) or the sum of the link cost c(i,j) plus cumulative cost w*(i) to the start-node. All links that have not been added to the MPT or deleted from further consideration (this occurs if the end node is reached via a shorter path) are considered for selection, not only the links just added. The minimum total cost (minimum temporary label) over all open nodes is always selected. |